World Models in Energy: AI‑Driven Decision Making for Complex Systems

Introduction

Many, if not most, decision-making problems have a sequential nature, i.e., decisions are made at each timestep and influence future choices. In this context, a well-established paradigm for decision-making is Model Predictive Control (MPC).

In MPC, each decision-making step involves projecting a sequence of future actions. A model is then used to evaluate this sequence by simulating the system dynamics and assessing the quality of the projected decisions. Typically, when an acceptable sequence of actions is found, only the first action in the sequence is implemented; after which the model is updated with the unfolded information. This process is repeated at every timestep to account for uncertainties, such as modeling errors.

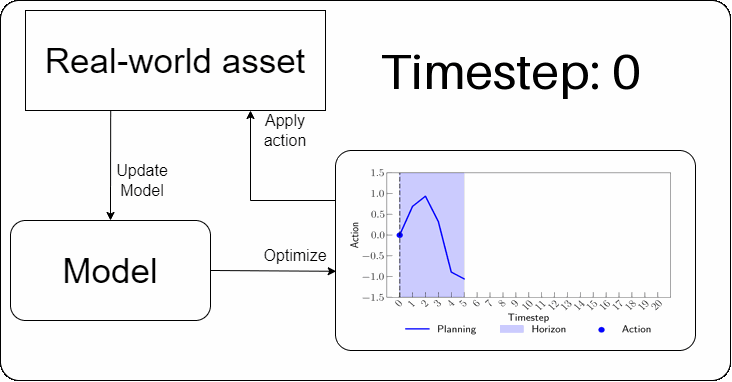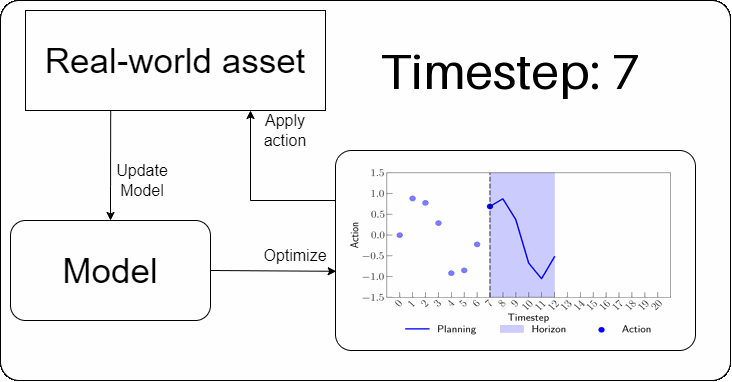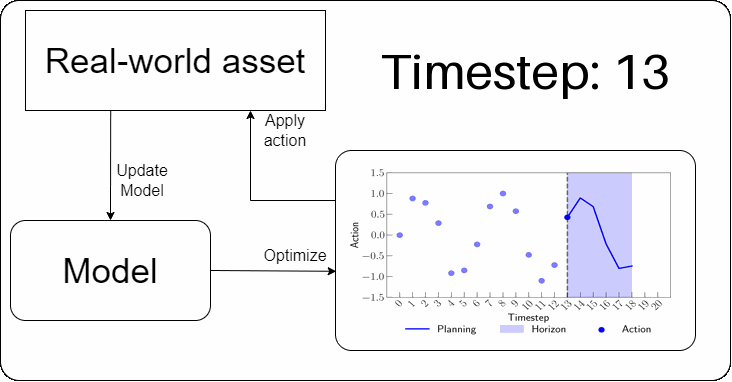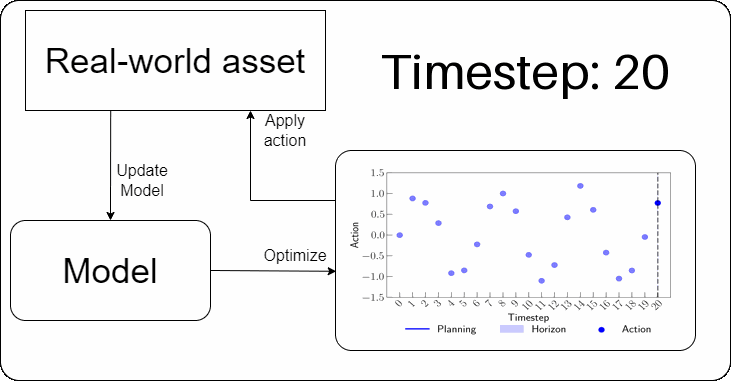
In practice, when MPC is viewed through the lens of operations research (e.g., [Camacho & Bordons; Diehl et al.]), it often boils down to solving an MILP-like problem at each decision step. This typically involves deriving a linear model using system identification techniques or based on first principles. However, recent advances in machine learning, high-performance computing, and data-driven decision-making have paved the way for more general approaches — Reinforcement Learning (RL) [Busoniu et al.] being a prominent example.

Data-Driven Methods

RL techniques are broadly categorized into model-based and model-free approaches. Model-free methods have achieved remarkable success in various domains—for example, in video games with the introduction of the Deep Q-Network (DQN) algorithm [Mnih et al.], and more recently in large language models (LLMs), where combining modern language architectures with the Proximal Policy Optimization (PPO) algorithm [Schulman et al.] enabled tools like ChatGPT.

These methods do not require an explicit model to derive a policy for sequential decision-making problems, hence the name. While model-free RL offers conceptual simplicity, it often demands large amounts of data and struggles to generalize beyond its training distribution.

When feasible, a more effective approach is model-based RL, which builds a system model using data-driven techniques. This model is then combined with a decision-making algorithm in an MPC-like fashion. Notable examples include PILCO [Deisenroth & Rasmussen], Dreamer [Hafner et al.], and MuZero [Schrittwieser et al.]. These methods incorporate generalized knowledge about the system, guiding RL algorithms toward more informed and efficient decisions.

An inspiring application is presented here  [Karpathy, 2022], where an approach is detailed for autonomous car driving. A network of cameras is used to build a 3D object map of the road, then a concentration of object maps is used in a recurrent network structure to make a model of how these objects move. Finally, this model is used in combination with a Monte Carlo Tree Search (MCTS)-like algorithm to schedule one’s car. 

World Models

A common feature of these approaches is the use of a world model: a learned representation that captures the dynamics of the environment in which the system operates and interacts. 

An important aspect of world models is that they typically consider and reason on a latent state, i.e., a low-dimensional representation crafted from high-dimensional observations such as a sequence of camera images [Ha & Schmidhuber].

A first very pragmatic reason to compress observations (as a proxy for a true state)  upon which the control policy acts is to mitigate the curse of dimensionality [Bertsekas] for decision making.

A second, slightly more nuanced reason is the premise that to describe the dynamics of a system with a high-dimensional observed state N (e.g., the pixels on a camera screen), one does not need a model that does a N → N mapping. For example, in the car driving application, one really needs to describe the dynamics of the main ‘features’ (e.g., other cars, pedestrians), not of every pixel.

By modeling the dynamics in a low-dimensional latent space extracted from high-dimensional observations, we can enable the world model to generalize the most relevant dynamics of the environment (i.e., what we are interested in to solve our control problem) with a neater representation. 

A clear example of this can be drawn from thermal dynamics, where we measure the kinetic energy of an extremely high number of particles forming a physical object with a single value: the temperature. Temperature describes the main information we are interested in knowing regarding the thermal dynamics of an object, and it does so in a very compact space, as opposed to the full set of information that would be impossible to compute.

Another more illustrative example comes from autonomous driving, where high-dimensional sensor data are mapped to structured representations of objects and their dynamics, and planning is performed using these learned dynamics [Karpathy, 2022].

This approach is intuitive for image-based observations, but its broader application assumes a hierarchy in model complexity, where essential features dominate system behavior.

A powerful example of the algorithmic application of a latent representation is present in the MuZero framework [Schrittwieser et al.]. MuZero approximates the dynamics of a sequential decision-making problem using an internal latent representation that is completely detached from the actual state representation of the system. This allows the algorithm to create a latent space that represents the problem in a syntax that is best exploited by the control agents.

What About the Field of Energy?

The energy sector is rich with sequential decision-making problems, ranging from long-term investment planning to short-term trading and real-time demand response activations. These challenges are inherently dynamic and require decisions that influence future states of the system. 

A key advantage in this domain is the abundance of data—although often fragmented across different sources and stakeholders—which creates opportunities for data-driven approaches such as reinforcement learning and world models.

Moreover, the energy sector is characterized by a well-understood and highly structured foundation. Physical assets follow universal laws—heat pumps obey thermodynamic principles, which remain consistent worldwide; market-clearing mechanisms optimize social welfare; and grid-connected assets adhere to power-flow equations.

This inherent structure makes the concept of a world model particularly powerful in energy applications. By combining rich data sources with established physical and economic principles, world models can potentially enable universal representations that generalize across contexts. These models, when paired with general-purpose solvers, offer a scalable way to tackle diverse sequential decision-making problems—from operational control to market optimization—while leveraging both data-driven insights and domain knowledge.

An example of such applicability can be drawn from a previous work of ours [Pavirani et al.]. There, we approximated the thermal dynamics laws of a residential building equipped with a heat pump using a physics-informed neural network. The model uses first-grade physical equations to build a compact yet information-rich state, which is then used by an MCTS-based technique to control the heat pump to minimize energy costs and thermal discomfort.

The use case considered can be scaled to a more universal world model, exploiting the universal laws of thermal dynamics with the common demand response market mechanism applied to modern electrical grids.

In summary, the convergence of data-driven methods and well-established physical and economic principles makes the energy sector an ideal candidate for world-model-based approaches. By leveraging latent representations and structured knowledge, these models can overcome the curse of dimensionality, improve generalization, and enable scalable solutions to complex sequential decision-making problems. As reinforcement learning and model-based techniques continue to evolve, world models offer a promising pathway toward more intelligent, efficient, and adaptive energy systems—bridging the gap between theory and real-world impact.

Current Work

At Beebop and within the AI4Energy (AI4E) team in Ghent, we are exploring and applying these ideas to develop scalable approaches for harnessing flexibility in energy systems. The focus is on combining structure and data in a way that supports robust, interpretable, and reusable decision-making methods.

-------------------------------

References

• Bertsekas, D. P. (2017). Dynamic programming and optimal control (Vols. 1–2). Athena Scientific.
• Busoniu, L., Babuska, R., De Schutter, B., & Ernst, D. (2010). Reinforcement learning and dynamic programming using function approximators. CRC Press.
• Camacho, E. F., & Bordons, C. (2007). Model predictive control (2nd ed.). Springer.
• Deisenroth, M. P., & Rasmussen, C. E. (2011). PILCO: A model-based and data-efficient approach to policy search. In Proceedings of the 28th International Conference on Machine Learning (ICML).
• Diehl, M., Bock, H. G., & Schlöder, J. P. (2005). A real-time iteration scheme for nonlinear model predictive control. In Nonlinear model predictive control (pp. 271–283). Springer.
• Ha, D., & Schmidhuber, J. (2018). World models. arXiv preprint arXiv:1803.10122.
• Hafner, D., Lillicrap, T., Norouzi, M., & Ba, J. (2020). Dreamer: Scalable reinforcement learning using learned world models. arXiv preprint arXiv:1912.01603.
• Karpathy, A. (2022). Tesla AI Day: Autonomy and neural networks [Presentation].
• Mnih, V., et al. (2015). Human-level control through deep reinforcement learning. Nature, 518, 529–533.
• Schrittwieser, J., et al. (2020). Mastering Atari, Go, Chess and Shogi by planning with a learned model. Nature, 588, 604–609.
• Karpathy, A. (2022). Tesla Autonomy AI Day.
• Schulman, J., et al. (2017). Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347.

‍